
ANNEX D.
This paper although it is considered to have some interest (from the mathematical and the paradigms points of view), is obsolete since 2011. See now the paper: redistribs_eterinicas_en.pdf
Example of REDISTRIBUTION.
Redistribution of aetherino speeds caused by a composite particle bathed by an isotropic aether.
A "Composite Particle" (CP) was defined in Section 1 as an ensemble of "Simple Particles" (SP) that keep confined in a "small" region of space. (In most cases this region will be considered "small" relative to the average separation between the other CPs of the problem. For example in this section the region occupied by the redistributing CP will be considered "small" relative to its separation with the target particle affected by such redistribution).
The calculus of the redistribution (caused by the CP due to the collisions of aetherinos with its SPs) will be based on the following:
- Hypothesis D: when an aetherino collides with a Simple Particle, the aetherino changes its velocity in such a way that, in the reference frame S' associated with the SP, the following relation is fulfilled:
vf = -vi + V [d-0]
where:
vi is the velocity of the incident aetherino in the reference frame S' in which the SP is initially at rest. (vi is therefore the velocity of the incident aetherino relative to the SP).
V is the velocity of the SP in S' after the collision. (V is therefore the velocity increase acquired by the SP as a consequence of the collision).
vf is the velocity of the aetherino in S' after the collision. (vf –V is therefore the velocity of the emerging aetherino relative to the SP after the collision).
Therefore the hypothesis D says that, in the reference frame in which the SP is initially at rest, the velocity of the aetherino relative to the SP after the collision is equal to minus the velocity of the aetherino relative to the SP before the collision. (Note: This hypothesis D expressed in [d-0] is different from the hypothesis D presented in version 1.5 (and earlier versions of this work). See note D-5 below).
The calculus of the redistribution will be done assuming the following idealized model of CP:
- All its component Simple particles have the same geometrical cross section s and they all move internally, relative to the global structure (CP) with the same speed w.
- The average separation of the SPs within the CP is much bigger than the "size" of a SP: i.e. the SPs do not screen each other sensibly from the incident aetherinos.
- All directions, relative to the CP, of the Simple particle’s velocities have the same probability to be found.

Consider a typical collision between an aetherino and a Simple particle. Let:
S reference frame associated to the Composite particle.
S' reference frame of the Simple particle considered.
v incident (initial) velocity of a colliding aetherino in S.
u emergent (final) velocity of the colliding aetherino in S.
vi incident velocity of the aetherino in S'.
vf emergent velocity of the aetherino in S'.
w velocity in S of the Simple particle considered.
q angle between w and v.
The velocity increase V acquired by the SP as a consequence of the collision is analysed (postulated) in Section 3 of this work. For the present deduction of the redistribution produced by the CP it will be assumed that:
V = g vi [d-0b]
where as before vi is the velocity of the aetherino relative to the SP before the collision and g is some constant.
Therefore the present assumption [d-0b] together with the hypothesis D (see d-0 above) implies:
vf = -vi + V = -vi + g vi = (g-1) vi [d-0c]
-------------------
NOTE D-0:
Assuming i
-------------------
The collision is represented in the following diagrams:
- In reference frame S before the collision:

- In reference frame S' (of the impacted SP):
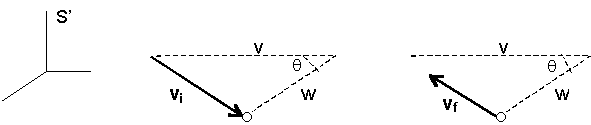
Before the collision After the collision
The final velocity u of the aetherino in S can be deduced from the following diagram:
 Fig [d-1]
Fig [d-1]
and therefore the speed u squared is:
![]()
![]()
![]() [d-1]
[d-1]
![]()
therefore:
 [d-2]
[d-2]
Let r(v) be the isotropic aetherino's distribution where the CP is located. (For simplicity the aether distribution is considered isotropic in the reference frame S associated with the CP).
r(v) = number of aetherinos with speed v in unit volume (per unit speed interval).
Consider first only those aetherinos of speed v that travel in a given semi direction of space.
The density of the selected aetherinos is r(v) / k where k is a (big) number of equal parts in which the totality of semi directions of space can be supposed to be divided.
The number of aetherinos of the selected type that collide in unit time with a given Simple particle of velocity w = {w, q} is:
 [D-3]
[D-3]
where:
s is the cross section of a Simple particle.
q
is the angle between the direction (in S) of the incident selected aetherinos and w.(v
2 +w2 -2vwCos q)1/2 is the speed of an incident aetherino relative to the SP and therefore is also the distance travelled in unit time by the Simple particle in the reference frame where the selected aetherinos are at rest.Let m be the total number of Simple particles making the CP. Remembering that it has been supposed above that all directions of the Simple particle’s velocities w (in the CP reference frame) have the same probability to be found, then, the number of aetherinos of the selected type that collide in unit time with all the Simple particles whose direction belongs to the interval {q , q + dq } is:
 [D-4]
[D-4]
In all of these collisions the colliding aetherinos emerge with the same speed u (in S).
But it can be seen (for example plotting the function u(q) deducible from [d-1]) that given u and v there exists at most a single value of q able to produce such speed u emergent aetherinos. This allows to express N(v,q) as a function of u instead of q :
Considering that du and dq are related (differentiating both sides of [d-2] with v taken as constant) by:
 [d-5]
[d-5]
(where g and w have of course also been considered constants) then Eq[D-4] may be rewritten as a function of u:
 [d-6]
[d-6]
f(v,u) du expresses the number of aetherinos that, having suffered a collision with any SP of the CP, emerge in unit time with speeds in the interval {u,u+du}, and that before such collision had a speed v in the direction chosen (one of the k). The emergent direction of these speed u aetherinos will later become unimportant since, by isotropy considerations of the local aether, when considering all the k possible directions of the incident speed v aetherinos, all directions of emergence must occur with the same probability. The speed v used in Eq [d-6] must not be bigger than a certain value v
Max nor smaller than a certain value vmin that allow the existence of a real q in Eq[d-2]. These limiting allowed values of v capable to produce speed u aetherinos are: [d-7]
[d-7]
Adding for all the incident aetherinos, whatever their speed v and whatever their direction (i.e. multiplying by k directions), that are capable of producing emergent aetherinos in the speed interval {u,u+du}, the number of these "produced" by the CP in unit time in all directions is:
![]()
 [d-8]
[d-8]
When wanting to evaluate the aetherinical force suffered by a distant body due to the presence of the CP (or more precisely, due to the redistribution produced by this CP) the calculus may be done (as was said in section 1) subtracting from the emergent distribution [d-8] those aetherinos that would reach the vicinity of the distant target body if the CP was not present. These aetherinos to be subtracted are just those that have suffered the collisions and redistribution accounted for in expression [d-8]. Its number can be calculated following the same line of reasoning as follows:
The number of aetherinos of speed v (in S) that, travelling initially in a given direction (one of the k), suffer collisions in unit time with Simple particles whose velocity forms (in S) an angle in {q , q+dq } with the given direction was expressed in [D-3]. When considering all the possible angles of the Simple particles with the given incident direction of the aetherinos such number increases to (see N(v,
q) in D-4):![]() [D-9]
[D-9]
When considering all the k possible incident directions the preceding quantity must be multiplied by k. Hence the total number of aetherinos of initial speed v, whatever their direction, suffering collisions in unit time with the composite particle (CP) is:
 [D-10]
[D-10]
 [D-10b]
[D-10b]
Distributions [d-8] and [D-10] express respectively the number of aetherinos "added" and "subtracted" in unit time to those existing in the aether.
The net "production" of speed u aetherinos in unit time is given by n
T(u)-sT(u) (where sT(u) is of course just sT(v) with a direct replacement of v by u). Dividing this number by 4p gives the number of speed u aetherinos "produced" by the CP by unit solid angle. This last quantity has been called "residual distribution" of the CP: [d-11]
[d-11]

(the distributions r(u), n(u) and s(u) are quantities by unit solid angle).
nT(u).du and sT(u).du have both the dimension T-
1. Therefore nT(u) and sT(u) have both the dimension L-1 .The name "redistribution" will also be used for a "residual" distribution.
Since the process of redistribution studied in this example does not assume any net source nor sink of aetherinos it must be understood that the words "produced", "added" or "subtracted" used in the preceding paragraph are only indicating transfer of quantities between the pertinent ensembles of aetherinos. It can be seen that:
![]() [D-12]
[D-12]
NOTE
The residual distribution [d-11] due to a non compact Composite Particle (at rest in the aether) whose SPs move at an internal speed w, will be rewritten swapping the variable names u and v to use the letter v for the speed of the aetherinos emerging from the CP as:
[1-45]

where g is an adimensional constant such that 0 < g < 1 and where
[1-46]

In those expressions w must be substituted by w
E if the redistributing source particle represents an electron or by wP if it represents a proton.The redistribution r(v) of [1-45] gives as usual the residual number of aetherinos of speed v (relative to the redistributing source particle) emerging from it by unit solid angle and by unit time.
r(v) is the canonical distribution i.e. the distribution of the local aether before being altered by the redistribution of the matter involved in the evaluation. Supposing that the canonical distribution is of the Maxwell-Boltzmann kind:[1-47]

which reaches its maximum for v = V
M and has the property that the total number of aetherinos in unit volume is constant no matter what is the value of VM.[1-47b] ![]()
it can be seen that r(v) has the form:
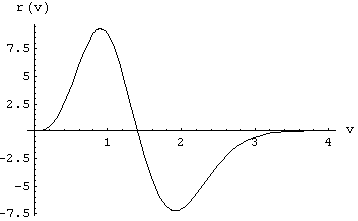
Fig [1-48]
w = 0.05, g = 0.01, N
0 = 104, VM= 1, m = 1, s = 1
For the plot of Fig [1-48] the following values have been arbitrarily assigned to the constants appearing in equations [1-45] and [1-47]:
w = 0.05
, g=0.01, N0 = 104, VM=1, m = 1, s = 1It is interesting to observe that using a higher value of w the redistribution [1-45] changes its form giving now instead a deficit of aetherinos for small speeds v and an excess for high speeds v. For example with:
w = 0.1
, g=0.01, N0 = 104, VM=1, m = 2, s = 1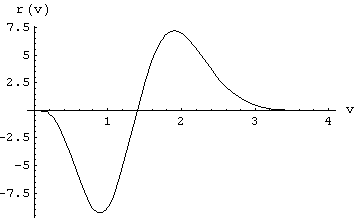
Fig [1-49]
w = 0.1, g = 0.01, N
0 = 104, VM=1, m = 2, s = 1In this second evaluation of r(v) the number m of Simple particles making the CP (source of the redistribution) has been chosen m=2 (instead of m=1). This has the effect to multiply the whole function by 2 and it then happens that the redistribution of Fig 1-48 is approximately the negative of the redistribution of Fig 1-49. It is in this line that the model aims to explain the hypothesis r
P(v) = - rE(v).Modelling both the proton and the electron as non compact Composite particles it has not been possible to find a pair of values w
E and wP with which to predict all the relations of [1-44b] FEE = -FPE = FPP = -FEP > 0(where F >0 means that F is a repulsive force).
and it is believed that at least one of these two elementary particles must be modelled by a compact Composite particle to succeed. Although the calculus has not yet been made in detail it can be hinted that the probability that the slow aetherinos incident on a compact target CP collide with any of its SPs is enhanced in comparison with the collision probability of aetherinos of fast speed relative to the target CP. This amounts to introducing a correction probability factor P(v
R) in the elementary impulse i1 = q vR (see Eq(1-0) of Section 1) produced by an aetherino on the Simple particles of a compact CP. It is believed that with this correction factor the force due to a source redistribution like that of Fig[1-49] can be seen to be attractive when acting on a compact CP while being repulsive when acting o a non compact CP. (Imagine for example that the electron is a compact CP redistributing according to the r(v) of Fig[1-48] and that the proton is a non compact CP redistributing according to the r(v) of Fig[1-49]).-----------------------
The aetherinical force exerted on a Simple particle (at rest relative to the source particle) has also been calculated for these 2 cases in which the residual distribution of the source is given respectively in Figs 1-48 and 1-49. Calling the residual distribution r(v), the force can be expressed (in analogy with the Eq[1-10] of the Section 1 of this work):

where
s is the geometrical cross section of the target Simple particle and where d is the distance between the redistributing source particle and the target Simple particle.Taking q=1, d=1,
s =1 it can be calculated that:F
1 = -3.53 for a source whose r(u) is that of Fig 1-48F
1 = +3.46 for a source whose r(u) is that of Fig 1-49A finer adjustment of the constants w and m of the two example redistributions should of course make the 2 forces exactly equal and opposite.
---------------
Note: The rest of this section belongs to the older version of this work and is kept here because there are references to it in other sections. It corresponds to a redistribution implicitely assuming that g=0 (see D-0b). It is now considered that g>0 is a more interesting case to study.
NOTE D1
An example of functions n(u), s(u) and r(u) has been represented in Fig [D-15] to give an idea of the redistribution caused by a CP according to this model. A Maxwell-Boltzmann speed distribution has been chosen to represent the environment canonical aether, i.e. in Eqs [D-8] and [D-10B] it has been assumed:
 [D-14]
[D-14]
which reaches its maximum for v = VM and has the property that the total number of aetherinos in unit volume is constant no matter what is the value of VM.

Fig [D-15] Redistribution of a CP.
Fig [D-15] of n(u), s(u) and r(u) corresponds to the following choices:
N0 = 1, m = 1, s = 1, w = 3, VM = 5
----------
NOTE D2
Some rough computations have been done to study the w (internal speed) dependence of the aetherinical force that a redistributing CP (source) exerts on a distant CP (target), both at rest in the local aether. Such force can be expressed (see an example in Eq[1-41] of section 1) as:
 [D-16]
[D-16]
where subindex S stands for "Source" and subindex T for "Target" and where:
mT = number of SPs of the target, wT = internal speed of the target SPs
rS(v) is the residual distribution of the source just calculated (Eq[D-11]) that depends on the internal speed w ( = wS) of the source SPs.
Using in [D-16] P(vR) = 1 (i.e. the simplest definition i1 = q vR f or the elementary aetherinical impulse (see [1-1]) and noticing that, according with the deduction of Eq[1-41] in section 1, vR = |v-wT| = ( v2 + wT2 - 2 v wT Cos q )1/2 it has been found that:
For a given VM and
for wT < VM, w < VM
and for a wT related to w by wT / w = k1 (k1 is an arbitrary constant)
![]() [D-17]
[D-17]
It has also been found that in the case of a shrinking canonical distribution (i.e. supposing that VM varies with time at the same rate as the speed of all aether dragged bodies and therefore at the same rate of w) the relation [D-17] is again valid (with a greater quantitative precision than in the case of no shrinking). (For a discussion about shrinking distribution see Section 3).
NOTE D3:
As can be seen in Fig[D-15] the above assumptions of redistribution have the consequence that a typical CP (at rest in the local aether) produces continuously an increase in the number of high speed aetherinos (of the surrounding aether) together with a decrease in the number of the slow speed ones. Therefore the presence of the CPs far from contributing to a shrinking (or "cooling") aether distribution (see Section 3) are causing just the opposite (i.e. "heating" the aether).
But if the model seeks to describe the existence of both positive and negative electric charges and therefore of attractive and repulsive forces between different kinds of material particles it must invoke the existence of other types of redistributing CPs and also, most probably, other assumptions related with the mechanism of redistribution. The model of CP used above in this Annex can be called a "diffuse CP" (i.e. the average separation of the SPs within the CP is much bigger than the "diameter" of a SP and hence its SPs do not screen (or shadow) each other sensibly from the incident aetherinos). It is believed that invoking also the existence of "compact CPs" in which the SPs do screen each other and doing the calculus of the redistribution it can probably be predicted the appearance of new residual distributions of the aether cooling type. (This calculus must probably allow for the fact that when an aetherino "enters" a compact CP it is likely that it suffers more than one collision with their SPs before exiting the CP). The calculus seems difficult and has been postponed. It also seems probable that the simplest explanation mechanism of gravitation is the recognition of an overall aetherino screening between any 2 macroscopic pieces of matter. Gravitation is analyzed in another section.
It may happen that the (postponed) calculus of the redistribution by a compact CP does not render the wanted prediction of a residual cooling distribution. (I.e. if r(u) is the above residual distribution of a diffuse CP it would be very satisfactory for the model if it could predict (with the same redistributing assumptions: hypothesis C, etc) that the redistribution of a compact CP is of the type rC(u) = - r(u). This would describe within the same paradigms the residual distributions of both the positive and negative charges).
It may even happen that not only such calculus fails to render the wanted prediction but that no other simple, convincing redistribution assumptions can be postulated to predict (within the ideas of the model) the existence of two types A and B of particle's redistributions such that rA(u) = - rB(u). Would that be the case, it is considered that this failure should not be considered by itself a powerful enough reason to abandon the model altogether. "Ad hoc" unexplained redistributions can always be introduced that could prove useful to make interesting descriptions and/or predictions within the paradigms of the model.
The following are examples of ad hoc redistributions:
Suppose a material particle A whose internal structure is ignored. Let sA be its geometric cross section. Suppose that A is at rest in a canonical aether. The number of incident aetherinos of speed u that A scatters by unit time is :
sA(u) = sA.r(u).u [D-21]
(as can be seen with a straightforward reasoning or alternately finding the limit of Eq[D-10b] when w tends to zero. Notice also that the v of Eq[D-10b] is now called u).
Suppose now ad hoc that each aetherino incident on A with a speed u, after being scattered emerges with a speed u/kA , where kA is a constant of the A-type particles. A unit speed interval of scattered aetherinos centred at the speed kAu generates (according to that supposition) aetherinos in a speed range no longer unity but equal to 1/ kA . Therefore a factor kA must be introduced to get a transformed distribution by unit speed interval . The emergent distribution exiting A is therefore:n
A(u) = kA sA(kAu) [D-22]where s
A(kAu) implies substituting in the expression [D-21] of the scattered distribution the variable u (whenever it appears) by kA u.The residual distribution of A is therefore
rA(u) = nA(u) - sA(u) = kA sA(kAu) - sA r(u) u == k
A sA r( kA u) kAu - sA r(u) u [D-23] where r is the canonical distribution [D-14]Suppose another type of particle called B for which is valid the same situation but whose "redistributing" constant k
B is different from kA.Using as the canonical aether distribution that given in Eq[D-14] with V
M=1 and N=1. Taking sA = sB =1 and taking (ad hoc) for example kA=1.04 and kB= 0.96 it can be seen that, as wanted, it is approximately rA(u) = - rB(u)
(the thick curve corresponds to the residual distribution of A (i.e. k
A=1.04) and the thin one to that of B).Graphics [D-15] and [D-24] have been created with the software "Mathematica" from Wolfram Research Inc.
Note: It has been found that the redistribution [D-11] deduced above can be approximated by a redistribution of the simpler ad hoc type given in Eq[D-23] if the internal SP' speeds w << VM. This approximation is: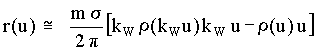
![]()
and where, as above, m is the number of SPs forming the redistributing CP, s is the geometric cross section of a SP and r is the canonical aether distribution that reaches its maximum for the aetherino speed V
M.-----------------------------------
NOTE D5:
In version 1.5 (and earlier ones) of this work a simpler hypothesis D was presented . Namely saying: vf = -vi independently of the velocity increase suffered by the collided SP. But assuming that a SP changes its velocity when collided by an aetherino then a further thinking reveals that such earlier hypothesis D is somehow asymmetric. (Assuming instead that the SP doesn’t change its velocity when collided by an aetherino has clearly no interest in the context of this work. For example hypothesis B in section 3 does assume such velocity change).
Such earlier hypothesis D was asymmetric in respect to a temporal inversion. For example:
Suppose that in a reference frame S, in which the SP is initially at rest, an aetherino with initial velocity {vX ,0,0} collides with the SP. Suppose that as a consequence of such collision the SP acquires the velocity {VX ,0,0} and that the aetherino inverts its velocity as supposed by the earlier hypothesis D. Graphically (in reference frame S):
Before the collision
![]()
After the collision
![]()
If time is reversed, the above sequence of events is seen as a different collision. (Graphically in the same reference frame S):
Before the collision 
After the collision
![]()
But this "inverted" collision does not satisfy the earlier hypothesis D as is evident observing the velocities of the aetherino in the reference frame S’ in which the SP is at rest before the collision. Graphically in reference frame S’:
The aetherino does not invert its velocity after this time reversed collision and therefore the earlier hypothesis D is unable to pass the time reversion test.
It is easy on the other hand to check that the new hypothesis D (about the aetherino behaviour after a collision) : vf = -vi + V is consistent with time reversion.
The new hypothesis D, except for the non interesting case V = 0, is different from the earlier hypothesis D. It can easily be checked that the new hypothesis D (see Eq[d-0]) conserves the time symmetry of aetherino collisions no matter what the velocity increase V acquired by the SP is postulated to be. Note: It seems plausible that V is some function of the velocity vi of the incident aetherino relative to the SP. For example section 3 of this work adopts the hypothesis B that V = k vi assuming therefore that V and vi are proportional and have the same direction. This is also what has been supposed in [d-0b] of this section. But this simple hypothesis B might also need to be revised to explain within the model the maximum number of experimental facts.